φ は『１』を生む

黄金比 φ をまとめますと、特徴の一つは「 φ は『１』を生む」ということです。

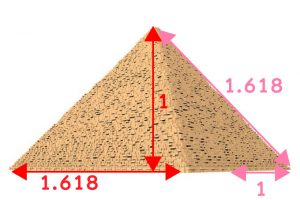
無理数 φ １．６１８０３３･･･を２乗すると、２．６１８０３３･･･、 φ ＋１となる ー

一方で、 １．６１８０３３･･･を１で割ると、０．６１８０３３･･･、 φ ー１となる ー

千々松健先生は「１．６１８を Φ （ラージファイ）、０．６１８を φ （スモールファイ）」とおっしゃっているので、それに倣いますと、 Φ × φ ＝１とも言えます。

Φ １．６１８０３３･･･　×　 φ ０．６１８０３３･･･　＝　１

【 Φ ^ 2 ー Φ  ＝１】　【 Φ ー φ ＝１】　【 Φ  ×  φ ＝１】

 φ は π を生む

一方で、 φ の渦は揺らぎの中で円周率 π を生み出します。

Φ ^ 2　÷  ５  ×　６　＝　 π

Φ ^ 2  ÷ ５ 　＝　π  ÷  ６　＝　Q（キュービット）０．５２３６

【Φ ^ 2  ÷ ５ 　＝　π  ÷  ６ 　＝　Q 】

【 π  ー  Φ ^ 2  ＝ Q  】

まとめ

黄金比 φ は『１』を生み、『 π 』を生む ー

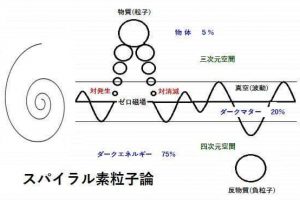
【 φ：Re 09】で『 π 』が物質と書きましたが、物質は『１』の方が的確かもしれません。

無限の無理数から『１』が生まれる、『個』が生まれる、『物質』が生まれる

とするなら、『 π 』は『生命』でしょうか。

φ の渦がつながって円となり、循環化する、その活動こそが『生命』活動。

長さと幅が φ であるDNAの２重螺旋構造が象徴するように、 φ が２乗となってその螺旋が循環する、陰陽ができて初めて生命が生まれる！？