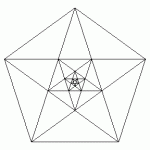
なぜ植物には★型が現れるのか?
通常リンゴは縦に切るので目にしにくいですが、横に切ると★型になるのをご存知ですか?
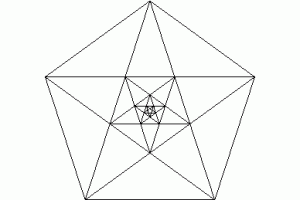
リンゴだけでなく胡瓜やウリ、オクラ等の実や、サクラをはじめ多くの花びらにも★型・五角形が現れますが、これはなぜなのでしょう。



これには、ゴールデンナンバー【 φ (ファイ)】が深くかかわっていると思うんです。
φが「不思議な数字である」という話は、前にしました。
思うに、植物や花に星型を出現させているのは実は φ であり、「すべてのモノは φ でできている」からではないか、というのがこのサイトの大きなテーマでもあります。
合わせて読む : 【ゴールデンナンバー【 φ 】①:不思議な無理数】
素粒子は φ でできている!?
物質の最小の単位は素粒子です。(ここまでは学術的)
そして、素粒子を構成しているのが φ なのではないか。(ここはたぶん学術的ではない)
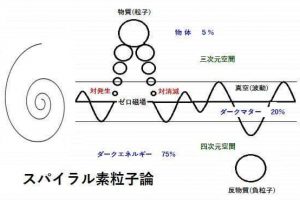
φ 、つまりそれは【流れ】であり、【運動】であり、その流れは【渦】を巻いていて三次元的には【螺旋】を形成している。
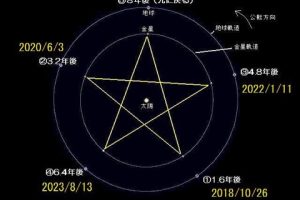
物質を象徴する【円】を φ で割ると、360 / φ = 223°となりますが、223°ずつ回転させていくと、下記のような図になります。(逆向きだと137° 360-223=137)

これは学術的には『葉序』といい、新しい葉は常に前の葉からほぼ同じ角度だけ回転した方向に生え、芽はどんな方向にも並ばずに効率よくスペースを満たすことができる、というものです。

このように仕向けているのが φ であり、そして、それは植物の成長だけではなく、ありとあらゆるところに見られるのです。
・自然は対数らせんが大好きだ
ひまわり・巻貝・水面にできる渦から台風や巨大な渦巻き銀河まで、まるで自然がこの驚くべき形状をお気に入りの装飾として選んだかのように見える。
どんな大きさのスケールでも対数らせんの形状が変わらないことは、自然界で有孔虫という単細胞生物や微化石の形にも見事に表れている。
この種の巻貝は複雑な構造をしているが、X線で撮影した化石の内部構造から、その対数らせんの形が何億年もほとんど変わっていないのがわかる・自然定数
我々の宇宙の性質は、原子の大きさから銀河の大きさまで、自然定数といういくつかの数値で決定されている。
この定数には、すべての基本的な力『重力・電磁気力・強い力・弱い力』の強さを決める尺度も含まれる。
たとえば二個の電子間に働く電磁力の強さは微細構造定数という定数によって物理的に表される。
この定数の値はなぜかほぼ正確に 1 / 137 で、これまで多くの物理学者を悩ませてきた。黄金比はすべてを美しくするか/Mario Livio
φ が π に変わる時・・・
この世は全て【 φ 】の流れでできていて、それが螺旋状に運動していて、それがある特異点に差し掛かり、球:【 π (パイ=円周率)】となって物質化する・・・
お互いに無理数であるゴールデンナンバー φ と円周率 π は、どこかで交わらないのだろうか、と考えて眺めてみました。

すると、どうでしょう。31416という円周率に近似する数字があるではありませんか!
これによると、 φ の2乗を5で割り6をかけると π となります。
φ^ 2 / 5 × 6 = π
上の公式を文章にしてみると、こんな感じでしょうか。
万物の根源である流れ【 φ 】の表・裏【2】が合わさり、それが四次元【5】から三次元【6】に変換されると物質【 π 】となる
この公式は、まさに物質とは何なのかを象徴しているのではないか・・・
ピラミッドの単位が・・・
遺伝子は2重螺旋構造でできていますが、これも φ そのものである気がします。
φ については引き続き追及していきますが、前回①の時の話につながる事実を一つ。
上記公式を変換すると下記になります。
φ^2 / 5 = π / 6
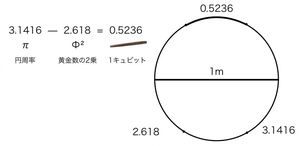
それは、φ の2乗を5で割ったものと、 π を6で割ったものはイコールである、ということであり、実際の数字は0.5236となります。
φ^2 / 5 = π / 6 = 0.5236
この0.5236、、実はこの0.5236という数字は、ピラミッドを作った時の単位【キュービット】なのです。
それは、古代人たちはこの数字を特別なものと考えていた、ということに他ならないのではないでしょうか。
合わせて読む : 【ゴールデンナンバー【 φ 】③: φ が物質となるイメージ】
合わせて読む : 【ゴールデンナンバー【 φ 】①:不思議な無理数】









コメントを残す